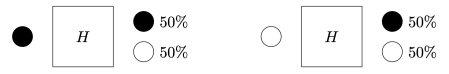The purpose of this post is to serve partly as a review of Terry Rudolph’s book Q is for quantum and partly as a record of my thoughts after a few months of reading about quantum computation. The first part of Ruldolph’s book may be downloaded for free from his website.
Part 1: Q-computing
The PETE box and the Stern–Gerlach experiment
Q is for quantum begins with a version of the Stern–Gerlach experiment. We are asked to imagine that black and white balls are sent through a box called ‘PETE’. (The afterword makes clear the name ‘PETE’ comes from Rudolph’s collaborator Pete Shadbolt.) After a black ball goes through a PETE box, it is observed to be equally likely to be black and white. The same holds for white balls.
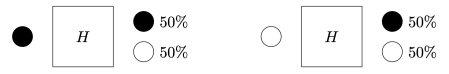
No physical experiment can distinguish the black balls that come out from the black balls that come in, or a white ball that comes out from a white ball from the supply of fresh balls. For example, if the white balls that come out are discarded, and the black balls that come out are passed through a second PETE box, then again the output ball is equally likely to be black and white.

The surprise comes when PETE boxes are connected so that a white ball put into the first one passes immediately into the second. Now the output is always white.
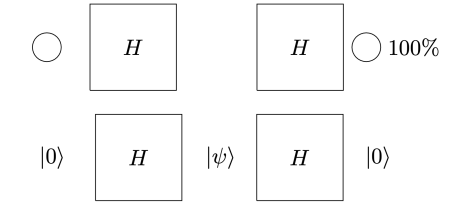
Naturally we are suspicious that, despite our earlier failure to distinguish balls output from PETE boxes from fresh balls, the first PETE box has somehow ‘tagged’ the input ball, so that when it goes into the second box, the second PETE box knows to output a white ball. When we test this suspicion by observing the output of the first PETE box, we find (as expected) that the output of the first box is 50/50, but so is the output of the second. Somehow observation has changed the outcome of the experiment.
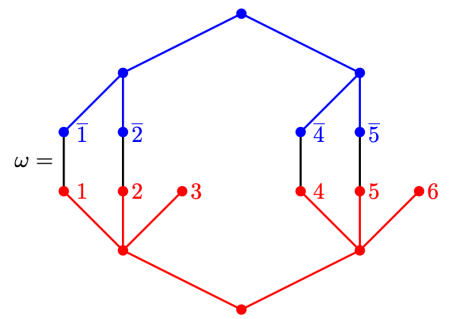
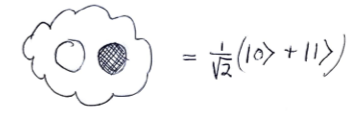
This should already seem a little surprising. But if we accept that observed balls coming out of PETE are experimentally indistinguishable from fresh balls then, Rudolph argues, we have to make a more radical change to our thinking: there is no way to interpret the state of an unobserved ball midway between two PETE boxes as either black or white. As Rudolph says, ‘We are forced to conclude that the logical notion of “or” has failed us’. This quickly leads Rudolph to introduce an informal idea of superposition and his central concept of a misty state. For example, the state 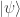 shown above is drawn as the diagram below.
shown above is drawn as the diagram below.
Rudolph then makes the bold step of supposing that when a black ball, represented by  is put through PETE, the output is
is put through PETE, the output is 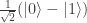 ; of course this is drawn in his book as another misty state, this time with a minus sign attached to the black ball. Does this minus sign contradict the experimental indistinguishability of output balls? I’ll quote Rudolph’s explanation of this point since it is so clear, even though (alas) it contains the one typo I found in the entire book (page 19):
; of course this is drawn in his book as another misty state, this time with a minus sign attached to the black ball. Does this minus sign contradict the experimental indistinguishability of output balls? I’ll quote Rudolph’s explanation of this point since it is so clear, even though (alas) it contains the one typo I found in the entire book (page 19):
But it isn’t a “physically different” type of black ball; if we looked at the ball at this stage we would just see it as randomly either white or black. No matter what we do, we won’t be able to see anything to tell us that when it we see it black [sic] it is actually “negative-black”.
In the mathematical formalism, this is the unobservability of a global phase (a consequence of the Born rule for measurement). Thus in a sense the PETE box does tag the black balls, but not in a way we can observe. The behaviour of a white ball sent into two PETE boxes in immediate succession is easily explained using superposition. The mathematical calculation
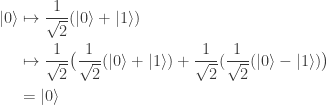
is not significantly shorter than Rudolph’s equivalent demonstration using misty diagrams on page 20. His book shows impressive economy by explaining many of the key ideas in quantum theory and computation using just these misty diagrams to compute with the PETE box and certain carefully chosen initial states.
Indeed, Rudolph has already shown one fundamental idea: if we accept that the misty state drawn above is a complete description (much more on this later) of a ball leaving a PETE box, then we have to give up on determinism. Instead the universe is fundamentally random. This was difficult for the early architects of quantum theory to accept, since it contradicts the idea that all physical properties have a definite value. Things are perhaps easier for us now: on the quantum side we are used to the uncertainty principle, and I’d argue that the complexity of modern life, and our relentless exposure to probabilistic and statistical reasoning, makes it easier for us to accept that randomness might be ‘hard-wired’ into the laws of physics. We return to these subtle points after the discussion of Part 2 of Rudolph’s book, where we follow Bell’s argument in refuting the ‘local hidden variable’ theory that, even though we cannot observe it for ourselves, PETE boxes are deterministic, and emit balls tagged in such a way that the laws of physics conspire to agree with the predictions from the misty state theory.
Translating from misty diagrams to the usual bra/ket formalism is of course routine. As one might hope, this infusion of mathematics has some advantages. For instance, if we accept the Born rule that measuring  in the orthogonal basis
in the orthogonal basis 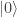 ,
, 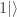 gives
gives 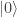 with probability
with probability 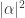 and
and 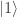 with probability
with probability  , then conservation of probability requires that this state evolves by unitary transformations in
, then conservation of probability requires that this state evolves by unitary transformations in  . Rudolph’s ‘bold’ step is now forced: once we have
. Rudolph’s ‘bold’ step is now forced: once we have
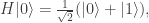
unitary dynamics requires that, up to a phase,
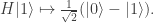
Thus, as my notation in the diagrams above suggests, the PETE box is the Hadamard gate
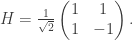
The Stern–Gerlach experiment shows further quantum effects which are not captured by Rudolph’s thought experiment. In the original experiment, silver atoms were sent through a magnetic field, strongest at the top of the apparatus and weakest at the bottom. The atomic number of silver is
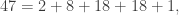
and correspondingly there is a single electron in the 4f subshell. The behaviour of the atom in the magnetic field in the experiment is determined by the spin of this electron. After passing through the magnetic field, two beams of atoms are observed: one deflected upwards and one deflected downwards. The amount of deflection is constant, showing the quantisation of the spin of this single electron.
Rudolph’s thought experiment corresponds to an extended version of this experiment, in which two different fields are used. Interpreting  as `spin up’, the diagram below shows atoms, prepared in the spin-up state by a vertical field, being deflected first by a horizontal magnetic field and then a second horizontal field in the combiner (this field has the reverse gradient to the first horizontal field), and finally a third vertical magnetic field identical to the first one.
as `spin up’, the diagram below shows atoms, prepared in the spin-up state by a vertical field, being deflected first by a horizontal magnetic field and then a second horizontal field in the combiner (this field has the reverse gradient to the first horizontal field), and finally a third vertical magnetic field identical to the first one.
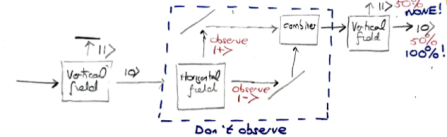
If the atoms are observed in the middle part of the apparatus (shown by a blue box above), or if one of the ‘mirrors’ indicated by diagonal lines is replaced with a barrier, then the output is 50%/50% (red text above). This is interpreted on the Wikipedia page as
… the measurement of the angular momentum on the  direction destroys the previous determination of the angular momentum in the
direction destroys the previous determination of the angular momentum in the  direction.
direction.
But if the atoms are not observed in the middle, then the output from the final vertical field is 100% spin-up, as for the output from the first vertical field. This holds even if the blue part of the apparatus, in which the horizontal field polarises electrons horizontally into two different beams, sends the atoms on a round trip of thousands of kilometres. As long as, they meet up at the combiner (without observation at any stage), the same interference occurs, and the output from the final vertical field is always spin-up. Since Rudolph’s thought experiment has no analogue of horizontal polarisation, this feature is not captured. But Rudolph has already made a convincing (and entirely honest) case that quantum phenomena cannot be understood by classical physics or conventional probability.
For a detailed account of the physics of the Stern–Gerlach experiment I found these notes useful. See Figure 6.9 for the experiment shown schematically above. Also I highly recommend this MIT lecture by Allan Adams for an entertaining and instructive treatment of the Stern–Gerlach experiment that has some features in common with Rudolph’s presentation, for instance, the use of colour to replace the spin-up and spin-down states  ,
,  ; he also brings in `hardness’ to replace horizontal polarisation and the states
; he also brings in `hardness’ to replace horizontal polarisation and the states 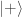 ,
,  seen in the blue part of the diagram above.
seen in the blue part of the diagram above.
Bank vaults and the Deutsch–Josaz algorithm
Part I ends with an illustration of quantum computing. We are asked to imagine that thieves have broken into a bank vault, in which each room is stocked with eight golden bars, numbered from  up to
up to 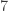 . In some rooms, all bars are fake (‘all that glistens is not gold’); in other rooms, there are four fake bars and four real bars. Happily each room has an ‘Archimedes’ machine, that given as input the ball sequence encoding the bar number in binary and one extra ball, flips the colour of the extra ball if and only if the bar is genuine. For example since
. In some rooms, all bars are fake (‘all that glistens is not gold’); in other rooms, there are four fake bars and four real bars. Happily each room has an ‘Archimedes’ machine, that given as input the ball sequence encoding the bar number in binary and one extra ball, flips the colour of the extra ball if and only if the bar is genuine. For example since  is
is  in binary, the input balls encoding
in binary, the input balls encoding  are black, black, white. We could use either colour for the extra ball. If we use white, then, supposing that bar
are black, black, white. We could use either colour for the extra ball. If we use white, then, supposing that bar  is genuine, the output is
is genuine, the output is
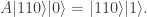
Moving the result from the  -basis
-basis  to the
to the  -basis,
-basis, 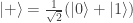 ,
,  we may rewrite this as
we may rewrite this as
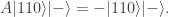
Less happily for them, the thieves only have time to use the Archimedes machine once. The ingenious solution is to apply Archimedes to a superposition of the numbers of all  bars, created by three white balls put into three PETE boxes in parallel, with the extra ball in the state
bars, created by three white balls put into three PETE boxes in parallel, with the extra ball in the state  , created by putting a black ball into a PETE box. The input is therefore
, created by putting a black ball into a PETE box. The input is therefore 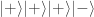 and the output is
and the output is
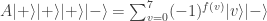
where 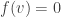 if bar
if bar  is fake, and
is fake, and 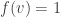 if bar
if bar  is genuine. If all bars are fake then the output is
is genuine. If all bars are fake then the output is
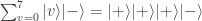
in agreement with the input. In this case, measuring in the  basis must give
basis must give 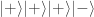 . Suppose instead that the vault has an even split. Since
. Suppose instead that the vault has an even split. Since
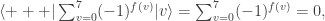
measuring in the  basis cannot give
basis cannot give  . Therefore one use of Archimedes suffices to distinguish the two classes of room.
. Therefore one use of Archimedes suffices to distinguish the two classes of room.
My account here differs from Rudolph’s only in measuring in the  -basis rather than applying a further three PETE boxes to move the first three balls back to the
-basis rather than applying a further three PETE boxes to move the first three balls back to the  -basis, where they can be measured (in the only way possible in his book) by inspecting their colour. This change replaces an operation with a computational flavour (applying three
-basis, where they can be measured (in the only way possible in his book) by inspecting their colour. This change replaces an operation with a computational flavour (applying three  gates in parallel) with mere linear algebra (just express the output in the
gates in parallel) with mere linear algebra (just express the output in the  -basis). Similary I prefer to think of the input as the product state
-basis). Similary I prefer to think of the input as the product state  in the
in the  -basis rather than as the result of four
-basis rather than as the result of four  gates applied to the product state
gates applied to the product state 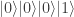 in the
in the  -basis. Of course this reflects my perspective that quantum computation is hard but (after 25 years of it) linear algebra is easy. The change of perspective is shown in the two circuit diagrams below.
-basis. Of course this reflects my perspective that quantum computation is hard but (after 25 years of it) linear algebra is easy. The change of perspective is shown in the two circuit diagrams below.

Rudolph can’t employ these dodges and instead gives a `proof by example’ for the even split case, using an alphabetic notation for the final misty state in the  -basis:
-basis:

with 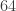 entries. The reader is invited to check that the coefficient of WWW is zero. With the exception of the final discussion of ‘ontic states’, this is probably the hardest part of the book, as clearly the author was aware, writing ‘Even if you raced through all that (as I would do on a first reading) and didn’t really follow it, that’s OK.’ Besides the jump in difficulty, a possible weakness of this section is the contrived nature of the problem. This however reflects the history of the subject: the Deutsch–Josaz algorithm was one of the earliest instances of quantum speed-up over classical algorithms. Rudolph illustrates this speed-up by considering a vault with 65536 gold bars.
entries. The reader is invited to check that the coefficient of WWW is zero. With the exception of the final discussion of ‘ontic states’, this is probably the hardest part of the book, as clearly the author was aware, writing ‘Even if you raced through all that (as I would do on a first reading) and didn’t really follow it, that’s OK.’ Besides the jump in difficulty, a possible weakness of this section is the contrived nature of the problem. This however reflects the history of the subject: the Deutsch–Josaz algorithm was one of the earliest instances of quantum speed-up over classical algorithms. Rudolph illustrates this speed-up by considering a vault with 65536 gold bars.
I think it is a little too tempting to conclude from Rudolph’s exposition that quantum computers are, at least for some tasks, strictly superior to classical computers. This however is unproved: the subtle point is that in any algorithmic specification of the problem, the Boolean function 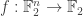 either has to be treated as an oracle, in which case the Deutsch–Josaz algorithm only proves the weaker result that relative to an oracle quantum computers are superior to classical computers, or given as part of the input, in which case it is no longer clear that there is no better classical algorithm than evaluating
either has to be treated as an oracle, in which case the Deutsch–Josaz algorithm only proves the weaker result that relative to an oracle quantum computers are superior to classical computers, or given as part of the input, in which case it is no longer clear that there is no better classical algorithm than evaluating  at
at 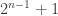 of the inputs.
of the inputs.
Still, this section is a nice illustration that quantum computers derive their power from interference, and not just (as Rudolph very clearly explains on page 50) from the superposition of exponentially many states. The reversible nature of quantum computing also emerges quite naturally from the white/black ball model and the use of the fourth ball in the input to Archimedes, but Rudolph chooses not to comment on this.
Part 2: Q-entanglement
This part, the highlight of the book for me, has an exceptionally clearly presented and improved version of the EPR-paradox. I’ll begin by giving my version of the original, separate from the more philosophical concerns of Einstein, Podolsky and Rosen, which I discuss in the final part.
The EPR-paradox as it seems now
Let 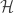 be
be  -dimensional Hilbert space modelling a single qubit, with
-dimensional Hilbert space modelling a single qubit, with  -basis
-basis 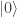 ,
,  . Alice and Bob have shared the Bell state
. Alice and Bob have shared the Bell state
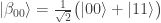
so that Alice has control of the first qubit and Bob the second. If all Alice and Bob can do is measure their qubit in the  -basis then
-basis then  behaves exactly like a shared (but unknown) classical bit: for each
behaves exactly like a shared (but unknown) classical bit: for each 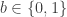 when Alice measures
when Alice measures  , she can be certain Bob will also measure
, she can be certain Bob will also measure  , and vice-versa.
, and vice-versa.
To motivate the next step we observe that  is not, as might seem from the formula above, in any way tied to the
is not, as might seem from the formula above, in any way tied to the  -basis. For instance, it is easy to check that
-basis. For instance, it is easy to check that
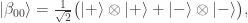
and in fact this formula holds replacing 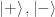 with any orthonormal basis of
with any orthonormal basis of 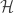 . It follows that Alice and Bob can measure in any pre-agreed basis
. It follows that Alice and Bob can measure in any pre-agreed basis 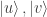 of
of 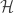 , and obtain the same classical bit. This suggests they might also try measuring in different bases. Let Alice’s basis (for the first qubit) be
, and obtain the same classical bit. This suggests they might also try measuring in different bases. Let Alice’s basis (for the first qubit) be
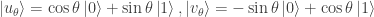
and let Bob’s basis (for the second qubit) be
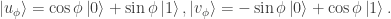
Thus Alice’s basis 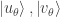 is obtained by rotating the
is obtained by rotating the  -basis by
-basis by  , and Bob’s basis
, and Bob’s basis 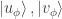 by rotating the
by rotating the  -basis by
-basis by  . It follows, by considering the inverse rotation, that
. It follows, by considering the inverse rotation, that 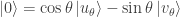 and
and 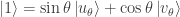 . There are of course similar expressions for the
. There are of course similar expressions for the  -basis elements in terms of Bob’s basis, obtained by replacing
-basis elements in terms of Bob’s basis, obtained by replacing  with
with  . Using these we obtain
. Using these we obtain
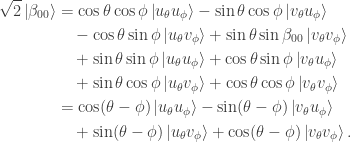
For instance if 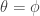 then
then 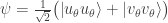 , so Alice and Bob either both measure
, so Alice and Bob either both measure  or both measure
or both measure  , as we claimed above. In particular, as already remarked, if Alice and Bob agree to measure in the
, as we claimed above. In particular, as already remarked, if Alice and Bob agree to measure in the  -basis, so
-basis, so 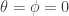 then when Alice measures
then when Alice measures  she can be sure Bob will also measure
she can be sure Bob will also measure 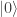 . If instead
. If instead 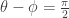 then the other two summands vanish and Alice measures
then the other two summands vanish and Alice measures  if and only if Bob measures
if and only if Bob measures 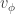 . If
. If 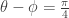 then there is no correlation between Alice’s measurement and Bob’s measurement. In particular, if Alice and Bob agree that Alice will measure in the
then there is no correlation between Alice’s measurement and Bob’s measurement. In particular, if Alice and Bob agree that Alice will measure in the  -basis and Bob will measure in the
-basis and Bob will measure in the  -basis then Bob is equally likely to measure
-basis then Bob is equally likely to measure 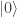 as
as  , irrespective of Alice’s measurement.
, irrespective of Alice’s measurement.
In general, by the Born rule, if 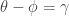 then the probability that Alice and Bob obtain the same result (i.e. either
then the probability that Alice and Bob obtain the same result (i.e. either  for Alice and
for Alice and  for Bob or
for Bob or 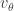 for Alice and
for Alice and 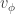 for Bob) is
for Bob) is 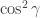 . All this leaves no doubt that Alice’s measurement affects Bob’s. This is the spooky ‘action at a distance’, or non-locality, that so bothered Einstein. We defer further discussion to Part 3, and instead present the main result from Bell’s 1964 paper, written 29 years after Einstein, Podolsky and Rosen.
. All this leaves no doubt that Alice’s measurement affects Bob’s. This is the spooky ‘action at a distance’, or non-locality, that so bothered Einstein. We defer further discussion to Part 3, and instead present the main result from Bell’s 1964 paper, written 29 years after Einstein, Podolsky and Rosen.
Bell’s game
We suppose that Alice and Bob are, as is usual in the tortured circumstances of thought experiments in quantum mechanics, held in isolated Faraday cages 20 light years apart. They are made to play the following game. The Gamesmaster chooses two classical bits and tells Alice 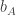 and Bob
and Bob  . Alice and Bob must each submit further classical bits
. Alice and Bob must each submit further classical bits 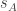 and
and 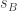 . They win if
. They win if  . That is, if
. That is, if 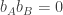 then Alice and Bob win if and only if they guess the same, and if
then Alice and Bob win if and only if they guess the same, and if 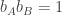 then Alice and Bob win if and only if they guess differently.
then Alice and Bob win if and only if they guess differently.
Using a single shared (but unknown) classical bit, or equivalently, by only measuring the Bell state in the same pre-agreed basis, Alice and Bob can win with probability 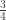 . One simple strategy is to ignore
. One simple strategy is to ignore 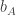 and
and  entirely and simply submit their shared classical bit. In this case
entirely and simply submit their shared classical bit. In this case 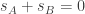 and our heroes win if and only if
and our heroes win if and only if 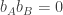 , which holds with probability
, which holds with probability 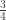 . In another strategy Alice submits
. In another strategy Alice submits 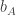 and Bob submits
and Bob submits  ; since
; since 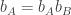 except when
except when 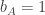 and
and  , again the winning probability is
, again the winning probability is 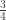 . (This strategy makes no use of their shared bit.) It is not hard to convince oneself that, provided the Gamesmaster plays optimally, for instance by choosing
. (This strategy makes no use of their shared bit.) It is not hard to convince oneself that, provided the Gamesmaster plays optimally, for instance by choosing 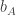 and
and  independently and uniformly at random, no better strategies are available. This holds even if Alice and Bob are allowed to use their own (independent, classical) sources of randomness before deciding what to submit.
independently and uniformly at random, no better strategies are available. This holds even if Alice and Bob are allowed to use their own (independent, classical) sources of randomness before deciding what to submit.
By measuring in different bases, Alice and Bob can do strictly better. It is clear that if Alice is told 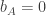 , she wants to choose a basis that must be close to Bob’s, while if Alice is told
, she wants to choose a basis that must be close to Bob’s, while if Alice is told 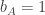 , then she wants a basis close to Bob’s when
, then she wants a basis close to Bob’s when  , and a basis rotated by nearly a right angle when
, and a basis rotated by nearly a right angle when 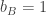 . Bob is of course in the same position. Thinking along these lines one can show that a good choice of bases for the measurements (each basis depending only on the classical bit each of them is told) is as follows:
. Bob is of course in the same position. Thinking along these lines one can show that a good choice of bases for the measurements (each basis depending only on the classical bit each of them is told) is as follows:
- For Alice: if
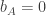 take
take 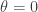 , if
, if 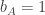 take
take 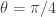 ;
;
- For Bob: if
 take
take  , if
, if 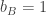 take
take 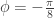 .
.
These bases are shown in the diagram below.
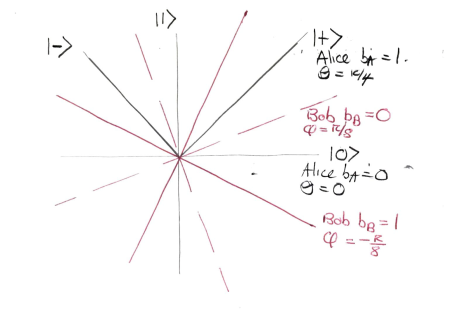
Note that Alice’s basis is the  -basis
-basis  when
when 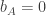 and the
and the  -basis
-basis 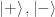 when
when 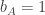 . This collection of all four bases is in fact the unique optimal configuration, up to rotations and reflections.
. This collection of all four bases is in fact the unique optimal configuration, up to rotations and reflections.
Checking the four cases for  shows that if
shows that if 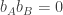 then the bases chosen by Alice and Bob differ by an angle of
then the bases chosen by Alice and Bob differ by an angle of 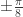 . Therefore Alice and Bob measure in nearby bases and submit identical bits with probability
. Therefore Alice and Bob measure in nearby bases and submit identical bits with probability 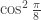 , winning with probability
, winning with probability  . If
. If 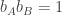 then the bases chosen by Alice and Bob differ by an angle of
then the bases chosen by Alice and Bob differ by an angle of 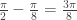 . The probability that Alice and Bob submit identical bits is now
. The probability that Alice and Bob submit identical bits is now  . Since their aim now is to submit different bits, they win again with probability
. Since their aim now is to submit different bits, they win again with probability  .
.
To give an explicit example, suppose that 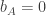 , so Alice measures in the
, so Alice measures in the  -basis, and
-basis, and  so Bob measures in the
so Bob measures in the  basis rotated by
basis rotated by  . The relevant form for
. The relevant form for  is
is
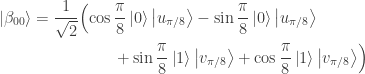
and so, as just claimed, the probability that either Alice measures 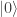 and Bob measures
and Bob measures 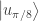 or Alice measures
or Alice measures 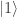 and Bob measures
and Bob measures 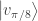 is
is 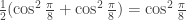 .
.
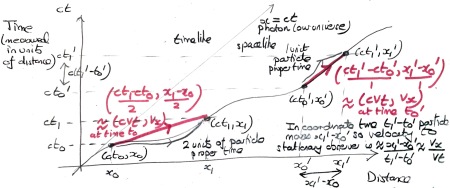
The Gamesmaster can arrange that Alice and Bob are told 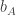 and
and  at the same time, and must then reply within a few seconds. (To take into account special relativity, we put Aice at the origin and Bob in a position space-like separated from Alice so that in any reference frame light takes more than the allowed number of seconds to travel from Alice to Bob.) This rules out even one way communication between Alice and Bob, unless they can employ a particle travelling faster than light. By applying a Lorentz transform one can convert any FTL-communication into a violation of causality. It is inconceivable that Alice’s qubit somehow transmits the result of Alice’s measurement to Bob’s qubit. But still, by choosing their bases carefully, Alice and Bob are able to influence the strength of the correlation (or anti-correlation) between their two measurements to the extent that they can play the game strictly better than classical physics allows. All this follows just from the Born rule for measurement and the simple rule proved above for how the Bell state transforms under two different rotations.
at the same time, and must then reply within a few seconds. (To take into account special relativity, we put Aice at the origin and Bob in a position space-like separated from Alice so that in any reference frame light takes more than the allowed number of seconds to travel from Alice to Bob.) This rules out even one way communication between Alice and Bob, unless they can employ a particle travelling faster than light. By applying a Lorentz transform one can convert any FTL-communication into a violation of causality. It is inconceivable that Alice’s qubit somehow transmits the result of Alice’s measurement to Bob’s qubit. But still, by choosing their bases carefully, Alice and Bob are able to influence the strength of the correlation (or anti-correlation) between their two measurements to the extent that they can play the game strictly better than classical physics allows. All this follows just from the Born rule for measurement and the simple rule proved above for how the Bell state transforms under two different rotations.
Rudolph’s improved version
To make a convincing demonstration of the improvement from the classical 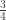 winning probability to
winning probability to 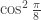 , Alice and Bob would of course have to play the game multiple times, and accept that they will lose with probability about 15%. For instance, after 100 trials with 85 successes, one would reject the null-hypothesis that Alice and Bob are using a classical strategy with confidence specified by the
, Alice and Bob would of course have to play the game multiple times, and accept that they will lose with probability about 15%. For instance, after 100 trials with 85 successes, one would reject the null-hypothesis that Alice and Bob are using a classical strategy with confidence specified by the  -value
-value  .
.
In Part 2, Rudolph offers an improved version of the EPR-paradox, using a game with three outcomes (win, draw, lose) in which, by using a suitable entangled  -qubit state, Alice and Bob can sometimes win and guarantee never to lose. Rudolph’s ingenious construction means that only measurements in the
-qubit state, Alice and Bob can sometimes win and guarantee never to lose. Rudolph’s ingenious construction means that only measurements in the  – and
– and  -basis are required, so (making the same shift from measurement-in-arbitrary-basis to computation-by-unitary-operator-and-
-basis are required, so (making the same shift from measurement-in-arbitrary-basis to computation-by-unitary-operator-and- -basis measurement remarked on earlier) Alice and Bob can work the magic using only black and white balls and the PETE box. Rudolph sets things up very carefully, in the entertaining context of Randi’s well known million dollar price for an experimentally testable demonstration of telepathy (or indeed, any psychic phenomenon). In particular, my claim above that no classical strategy can beat
-basis measurement remarked on earlier) Alice and Bob can work the magic using only black and white balls and the PETE box. Rudolph sets things up very carefully, in the entertaining context of Randi’s well known million dollar price for an experimentally testable demonstration of telepathy (or indeed, any psychic phenomenon). In particular, my claim above that no classical strategy can beat 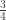 in the EPR-game becomes the claim that any classical strategy in Rudolph’s game that has a non-zero winning probability also has a non-zero losing probability: this is convincingly shown in the narrative.
in the EPR-game becomes the claim that any classical strategy in Rudolph’s game that has a non-zero winning probability also has a non-zero losing probability: this is convincingly shown in the narrative.
Part 2 ends with a discussion of just what is paradoxical about the games. Rudolph argues that a causal explanation of the nonlocal correlation in misty states is inconsistent with our understanding that causes precede effects, and that information cannot be transmitted faster than light. He remarks ‘physicists seriously consider other disturbing options’, for instance the super-deterministic theory where the bits 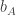 and
and  and Alice and Bob’s strategy (and even, whether or not Alice and Bob will follow their strategy as instructed) are already ‘known’ to the entangled qubits. Another possibility is that Rudolph’s ‘misty state’, modelling the two entangled qubits, is in fact ‘some kind of real physical object like a radio wave or a bowl of soup, and when we separate the psychics the mist is stretched between them’. (Rudolph is very clear that until this point, the misty states have been a mathematical abstraction, just as my calculations with unitary matrices above.)
and Alice and Bob’s strategy (and even, whether or not Alice and Bob will follow their strategy as instructed) are already ‘known’ to the entangled qubits. Another possibility is that Rudolph’s ‘misty state’, modelling the two entangled qubits, is in fact ‘some kind of real physical object like a radio wave or a bowl of soup, and when we separate the psychics the mist is stretched between them’. (Rudolph is very clear that until this point, the misty states have been a mathematical abstraction, just as my calculations with unitary matrices above.)
Part 3: Q-reality
It is both a strength and weakness of Q is for quantum that at this point it is very tempting to throw up one’s hands and say ‘okay, I’m convinced misty states are the best approximation to reality there is, non-locality and paradoxical behaviour accepted’. I think this is particularly tempting for mathematicians — surely a theory of such beauty and explanatory power has to be ‘right’? As a partial corrective to this, let me break from following Rudolph’s book, and instead consider the EPR-paradox in its historical context. We follow this with a discussion of quantum teleportation, before rejoining Rudolph’s final chapter.
Rocky states and the EPR-paradox as presented by the authors
At the end of Part 2, Rudolph introduces the idea of a ‘rocky state’, namely a classical probability distribution on physical states. He shows that the entanglement in the Bell state  cannot be explained in this way: in mathematical language, a classical probability distribution that gives some probability to the observations
cannot be explained in this way: in mathematical language, a classical probability distribution that gives some probability to the observations  and
and 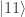 for both Alice and Bob must give a non-zero probability to
for both Alice and Bob must give a non-zero probability to 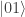 , but this has coefficient zero in
, but this has coefficient zero in 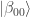 . This supports his conclusion that quantum theory (rather than classical probability) is required to explain the EPR-paradox.
. This supports his conclusion that quantum theory (rather than classical probability) is required to explain the EPR-paradox.
Whatever the status of misty states, rocky states are certainly epistemic: on page 103 early in Part 3, Rudolph writes `the rocky states are unquestionably representing our knowledge’. For example, if I borrow a coin from Malcolm and flip it on a table, and see roughly how far it is from the edge, my rocky state might be as shown left below. Malcolm however knows his coin is double-headed, so his rocky state is as shown on the right.
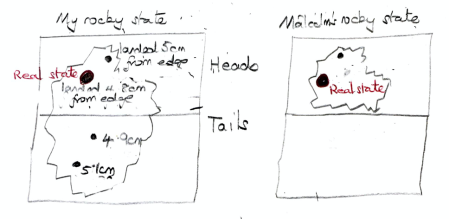
As Rudolph writes (page 104),
the very fact that two different rocky states can correspond to the same real state indicates that the rocky states themselves are not a physical property of the coin.
So far, so clear, I hope. It is therefore striking that a very similar argument led Einstein, Podolsky and Rosen to conclude that misty states could not be in bijection with real states. To understand this, I think one must first appreciate that the authors took at one of the starting points in their paper that particles had real physical properties that were revealed by observation. Some version of this view, ‘scientific realism’, is implicit in the scientific method, and helps to explain its power. (We used it earlier, when we deduced from the experimental indistinguishability of balls output by the PETE box from fresh balls that there was a fundamental randomness in the laws of physics.) As a working definition, let me define naive realism to mean that an output ball from a PETE box is definitely either black or white — we just don’t know what it is until observation. Equivalently, the  -basis state
-basis state  is a convenient mathematical representation for a real state that, on observation, turns out to be either
is a convenient mathematical representation for a real state that, on observation, turns out to be either  or
or 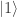 . Thus, in naive realism, quantum states are incomplete descriptions of real states, and the real states have deterministic non-random behaviour.
. Thus, in naive realism, quantum states are incomplete descriptions of real states, and the real states have deterministic non-random behaviour.
Suppose as in the exposition of the EPR-paradox in Part 2, that Alice and Bob share the entangled Bell state  , but now separated by (let us say) 10 light seconds, and that Bob refuses to measure until he hears that Alice has done so. Suppose that Bob always measures in the
, but now separated by (let us say) 10 light seconds, and that Bob refuses to measure until he hears that Alice has done so. Suppose that Bob always measures in the  -basis. We saw that if Alice also measures in the
-basis. We saw that if Alice also measures in the  -basis then Alice and Bob are guaranteed to get the same
-basis then Alice and Bob are guaranteed to get the same  -basis measurement, while if Alice measures in the
-basis measurement, while if Alice measures in the  -basis, Bob is equally likely to get
-basis, Bob is equally likely to get 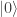 as
as 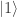 , whatever Alice measures. This agrees with the predictions of the extended version of the Born rule dealing with a measurement on just one qubit in an entangled system. In detail, if Alice measures in the
, whatever Alice measures. This agrees with the predictions of the extended version of the Born rule dealing with a measurement on just one qubit in an entangled system. In detail, if Alice measures in the  -basis
-basis
- and gets
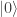 then Bob’s qubit is in the state
then Bob’s qubit is in the state 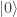 and Bob measures
and Bob measures  ,
,
- and gets
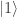 then Bob’s qubit is in the state
then Bob’s qubit is in the state 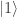 and Bob measures
and Bob measures 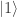 .
.
If Alice measures in the  -basis
-basis
- and gets
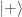 then Bob’s qubit is in the state
then Bob’s qubit is in the state  and, by the Born rule, Bob is equally likely to measure
and, by the Born rule, Bob is equally likely to measure  as
as 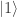 ;
;
- and gets
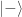 then Bob’s qubit is in the state
then Bob’s qubit is in the state 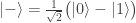 and, by the Born rule, Bob is equally likely to measure
and, by the Born rule, Bob is equally likely to measure  as
as 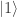 .
.
Thus depending on Alice’s measurement, the vector in Hilbert space (equivalently one of Rudolph’s ‘misty states’, or the ‘wavefunction’ in the language of the EPR paper) describing Bob’s qubit may take two different values. Except for changing ‘position’ to  -basis and ‘momentum’ to
-basis and ‘momentum’ to  -basis, this is the same situation as on page 779 of the EPR paper, where the authors write
-basis, this is the same situation as on page 779 of the EPR paper, where the authors write
We see therefore that as a consequence of two different measurements performed upon the first system, the second system may be left in states with two different wavefunctions. On the other hand, since at the time of measurement the two systems no longer interact, no real change can take place in the second system in consequence of anything that may be done to the first system. This is, of course, merely a statement of what is meant by the absence of an interaction between the two systems. Thus, it is possible to assign two different wavefunctions … to the same reality (the second system after the interaction with the first).
The authors conclude that the wavefunction is, like the rocky state of the flipped coin above, an incomplete description of reality. Repeating Rudolph’s argument from page 104 quoted above, since two different rocky states correspond to the same real state, the rocky state cannot be a physical property of the coin. This is consistent with (but does not imply in its full strength) naive realism.
The expectation of the EPR authors, if I understand the history correctly, was that quantum mechanics would be subsumed by a larger theory — maybe with ‘hidden variables’ — whose states would, everyone could agree, be in bijection with physical reality. Even the term ‘hidden variable’ now seems pejorative, but this idea of a progression of understanding by a sequence of more and more refined theories is of course entirely consistent with the history of physics.
Note the quote makes it very clear that the EPR authors do not regard Alice’s act of measurement as an interaction with Bob’s qubit. This assumption should seem doubtful given the game discussed in Part 2, where we saw that the improvement in the winning chance from 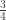 to
to 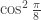 depended on Alice and Bob being able to influence the correlation between their measurements of their shared Bell state by careful choice of bases, using only locally available information. Indeed Bell’s 1964 paper concludes that this improvement is inconsistent with a local hidden variable theory:
depended on Alice and Bob being able to influence the correlation between their measurements of their shared Bell state by careful choice of bases, using only locally available information. Indeed Bell’s 1964 paper concludes that this improvement is inconsistent with a local hidden variable theory:
In a theory in which parameters are added to quantum mechanics to determine the results of individual measurements, without changing the statistical predictions, there must be a mechanism whereby the setting of one measuring device can influence the reading of another instrument, however remote. Moreover, the signal involved must propagate instantaneously, so that such a theory could not be Lorentz invariant.
This puts us back where we were at the end of Part 2, forced to accept the spooky ‘action at a distance’ effect of measuring. This non-locality was the central problem for Einstein with the theory: on the inability to measure Bob’s qubit in both the  – and
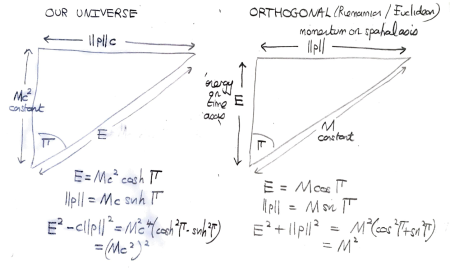
– and  -bases he wrote `es ist mir wurst’ (literally, ‘it is a sausage to me’). I’m happy to agree: I think scientific realism can easily stretch to accommodate measurements whose precision is limited by the uncertainty principle, and even to ruling out as simply nonsensical the idea of measuring both the position and momentum of a particle at the same instant. (Like the
-bases he wrote `es ist mir wurst’ (literally, ‘it is a sausage to me’). I’m happy to agree: I think scientific realism can easily stretch to accommodate measurements whose precision is limited by the uncertainty principle, and even to ruling out as simply nonsensical the idea of measuring both the position and momentum of a particle at the same instant. (Like the  – and
– and  -matrices, position and momentum are conjugate Hermitian operators.) More worrying perhaps, we are left with no better candidates for the ultimate elements of reality that Rudolph’s misty states. Rudolph admits the problems (page 81):
-matrices, position and momentum are conjugate Hermitian operators.) More worrying perhaps, we are left with no better candidates for the ultimate elements of reality that Rudolph’s misty states. Rudolph admits the problems (page 81):
Such a mist would … have to have many physical properties that differ from any other kind of physical stuff we have ever encountered. It would be arbitrarily stretchable and move instantaneously when you whack it at one end, for example. The whole question of how to interpret the mist—as something physically real? as something which is just mathematics in our heads?—is one of the major schisms between physicists.
I would have liked to see it mentioned here that even if Alice’s measurement does, as experimentally verified, instantaneously affect Bob’s qubit, it appears to be impossible to use this effect to transmit information. To be fair, Rudolph does consider this point carefully, but only later in Part 3. This distinction is particularly relevant in the context of quantum teleportation, which I discuss next.
Quantum teleportation
Most accounts of quantum teleportation that I have seen begin with the circuit below.
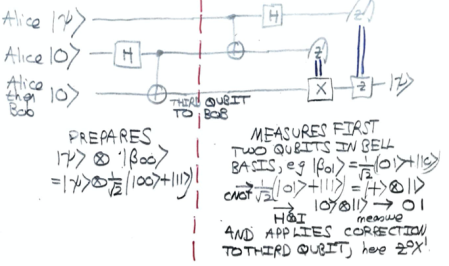
Alice begins in control of three unentangled qubits. The first is in the state 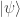 that she wants to teleport to Bob. After applying the Hadamard and CNOT gates, Alice sends the third qubit to Bob. She then applies another CNOT gate, a Hadamard gate and measures her two qubits in the
that she wants to teleport to Bob. After applying the Hadamard and CNOT gates, Alice sends the third qubit to Bob. She then applies another CNOT gate, a Hadamard gate and measures her two qubits in the  -basis. (Why?, you might well ask.) She sends the two classical bits that are the results of her measurements to Bob by a classical channel, marked as double blue lines in the diagram. Finally Bob applies a correction by
-basis. (Why?, you might well ask.) She sends the two classical bits that are the results of her measurements to Bob by a classical channel, marked as double blue lines in the diagram. Finally Bob applies a correction by  and
and  gates and, as if by magic, obtains
gates and, as if by magic, obtains  .
.
I think I would have got the idea rather more quickly if the circuit diagram had been accompanied by the explanations below:
- The circuit left of the red dashed line prepares the Bell state
 on the second and third qubits.
on the second and third qubits.
- The CNOT gate and Hadamard gate on the right of the red dashed line transform the Bell basis to the
 -basis. One example is shown above, another is
-basis. One example is shown above, another is 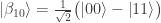 which is sent by the CNOT gate to
which is sent by the CNOT gate to 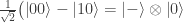 and then by the Hadamard gate to
and then by the Hadamard gate to 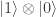 .
.
- By the identity
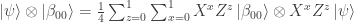
when Bob applies the corrections from the classical bits sent by Alice, he obtains  . (Note there is no ambiguity in
. (Note there is no ambiguity in  because
because 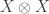 and
and  stabilise
stabilise  . This identity follows easily from the calculations on page 83 of Quantum computing: A gentle introduction by E. Rieffel and W. Polak.)
. This identity follows easily from the calculations on page 83 of Quantum computing: A gentle introduction by E. Rieffel and W. Polak.)
Since learning the rudiments of the ZX-calculus, I also find the graphical proof that the circuit behaves as claimed quite satisfying. Note in particular that the Bell state is simply the cup (shown horizontally) on the left of the dashed red-line.
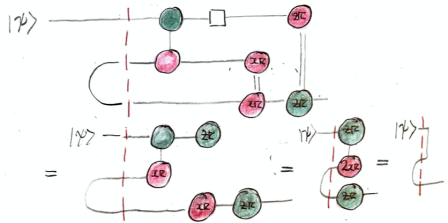
The algebraic view of the ‘yank’ that simplifies the ZX-calculus diagram is the identity
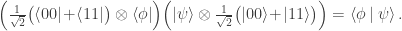
See (36) and (37) in ZX-calculus for the working computer scientist by John van de Wetering for more on this.
It is not hard to convince oneself that Bob cannot learn anything by observing the state 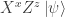 unless he knows at least one of the classical bits
unless he knows at least one of the classical bits  and
and  sent to him by Alice. For instance, if
sent to him by Alice. For instance, if  is known by all to be a
is known by all to be a  -basis element
-basis element  then Bob needs
then Bob needs  . (And in this case Alice might as well have sent the bit
. (And in this case Alice might as well have sent the bit  to Bob directly.) Thus while we believe that Alice’s measurements instantaneously affect Bob’s qubit, Bob cannot learn any information until light from Alice can reach Bob. This can be made precise using density matrices: the density matrix for Bob’s qubit is the uniform linear combination of the rank 1 density matrices for the four post-measurement states of the third qubit in the quantum teleportation protocol, namely
to Bob directly.) Thus while we believe that Alice’s measurements instantaneously affect Bob’s qubit, Bob cannot learn any information until light from Alice can reach Bob. This can be made precise using density matrices: the density matrix for Bob’s qubit is the uniform linear combination of the rank 1 density matrices for the four post-measurement states of the third qubit in the quantum teleportation protocol, namely
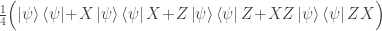
Setting 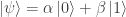 this becomes
this becomes
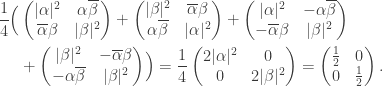
The right-hand side is the density matrix for the second qubit in the Bell state 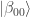 and is maximally uninformative: measurement in any orthonormal basis gives each basis vector with equal probability
and is maximally uninformative: measurement in any orthonormal basis gives each basis vector with equal probability  .
.
In addition, quantum teleportation appears to be consistent with naive realism as defined above. Let 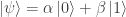 and think of
and think of  as a qubit that is
as a qubit that is  with probability
with probability 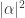 and is
and is 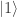 with probability
with probability  . At the end of the protocol, this probability distribution is transferred from Alice’s qubit to Bob’s qubit. This is consistent with the idea that the qubit has a definite, but unknown state, to which this probability distribution refers.
. At the end of the protocol, this probability distribution is transferred from Alice’s qubit to Bob’s qubit. This is consistent with the idea that the qubit has a definite, but unknown state, to which this probability distribution refers.
In a classical analogue (which I learned from Prof. Ruediger Schack) this transfer of probability distributions can, and in fact must be interpreted entirely epistemically. The analogue of the Bell state is two coins in unknown but equal states: imagine Alice tapes coin 2 to coin 3, flips the composite coin, and then without looking at either coin, keeps coin 2, and gives coin 3 to Bob. The analogue of  is a classical probability distribution on coin 1. In the protocol, Alice performs a parity measurement by performing another ‘tapped together flip’ on coins 1 and 2. She then looks at them both, and learns whether they are ‘same’ or ‘different’. She reports this to Bob, who then flips coin 3 if and only if Alice reports ‘different’.
is a classical probability distribution on coin 1. In the protocol, Alice performs a parity measurement by performing another ‘tapped together flip’ on coins 1 and 2. She then looks at them both, and learns whether they are ‘same’ or ‘different’. She reports this to Bob, who then flips coin 3 if and only if Alice reports ‘different’.
Alice’s probability distribution now refers to coin 3: if Alice believed that coin 1 was heads with probability  then she should now believe that Bob’s coin 3 is heads with probability
then she should now believe that Bob’s coin 3 is heads with probability  . To show the epistemic character of this, imagine that coin 1 is prepared by a coin toss performed by Alice’s assistant Charlie, and that Alice does not look at the coin until after the parity measurement. If the coin is fair then Alice’s probability is
. To show the epistemic character of this, imagine that coin 1 is prepared by a coin toss performed by Alice’s assistant Charlie, and that Alice does not look at the coin until after the parity measurement. If the coin is fair then Alice’s probability is  , but Charlie’s probability is either
, but Charlie’s probability is either  or
or  . In each case, this probability refers to coin 3 at the end of the protocol. Even though
. In each case, this probability refers to coin 3 at the end of the protocol. Even though  can be any real number in the interval
can be any real number in the interval ![[0,1]](https://s0.wp.com/latex.php?latex=%5B0%2C1%5D&bg=ffffff&fg=333333&s=0&c=20201002) , it may now seem that no information is teleported, except the single classical bit from Alice’s ‘same’ or ‘different’.
, it may now seem that no information is teleported, except the single classical bit from Alice’s ‘same’ or ‘different’.
I think this makes it all a little more plausible that quantum states are incomplete descriptions of a deterministic theory, and that while this theory must include instantaneous ‘actions at a distance’ effects, it could be that such effects cannot be used to convey information, and so do not (from our human perspective) violate causality. And while we saw in the discussion of the PETE box in Part 1, that the realist point of view that qubits have a definite state — we just don’t know what it is until observation — requires hidden variables, the asymmetry between Alice and Charles seen above, and the epistemic interpretation of the ‘teleportation’, shows that the existence of such hidden information by no means impossible.
Discussion of Part 3
Rudolph begins this part by explaining that if misty states are real then the behaviour of the PETE box can be explained: for example the  -basis state
-basis state 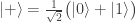 models a white ball output by a PETE box; if the next PETE box can ‘see’ this state then it can of course output a white ball in response. (That this happens by linear unitary evolution is nice for mathematicians, but potentially misleading: while linearity means we only have to state the effect of the Hadamard transformation on basis vectors, the behaviour of the PETE box, or rather the Stern–Gerlach magnetic fields, on superpositions is a property of the physical theory.) He also notes that this hypothesis does not require that misty states are a complete description of physical states.
models a white ball output by a PETE box; if the next PETE box can ‘see’ this state then it can of course output a white ball in response. (That this happens by linear unitary evolution is nice for mathematicians, but potentially misleading: while linearity means we only have to state the effect of the Hadamard transformation on basis vectors, the behaviour of the PETE box, or rather the Stern–Gerlach magnetic fields, on superpositions is a property of the physical theory.) He also notes that this hypothesis does not require that misty states are a complete description of physical states.
The difficulty with this hypothesis is of course observation: why can PETE boxes observe  -basis states without collapse, while human observation collapse everything we see into the
-basis states without collapse, while human observation collapse everything we see into the  -basis? We have seen that this act of observation requires instantaneous ‘action at a distance’ effects. Rudolph mentions attempts to make measurement compatible with unitary dynamics, writing (page 113)
-basis? We have seen that this act of observation requires instantaneous ‘action at a distance’ effects. Rudolph mentions attempts to make measurement compatible with unitary dynamics, writing (page 113)
But there are some models which work (at least for the ball type experiments we have considered; making them work for all experiments we can presently do is more tricky), and which soon will be experimentally ruled in or out.
Unhelpfully, no more details are given. He also mentions the ‘many worlds interpretation’ in which measurement splits the universe in two, in which the observer becomes a gigantic misty state representing a superposition of ‘observer saw black’ and ‘observer saw white’.
Next Rudolph considers the epistemic idea that misty states are ‘features of our knowledge, rather than real states of the world’ (page 115). He gives the argument from the EPR paper that since Alice’s measurement of her qubit in the entangled Bell pair can leave Bob’s qubit in two different misty states, and assuming that these measurements do not affect the physical properties of Bob’s qubit, two different misty states correspond to the same physical state, and so misty states cannot be physical properties. We saw above that the improvement from 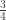 to
to 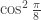 in the winning probability for Bell’s game makes this assumption very doubtful; Rudolph makes the same point very clearly using his improved version of Bell’s game.
in the winning probability for Bell’s game makes this assumption very doubtful; Rudolph makes the same point very clearly using his improved version of Bell’s game.
Rudolph goes on to illustrate, as usual in his toy model of black and white balls and PETE boxes, that measurements on an entangled Bell pair cannot be used to send information, by giving a special case of the calculation with density matrices above. The section concludes (page 126)
All this is mainly strange if you consider the mist to be real—if you follow Enstein and deny that the real state of Bob’s ball is changing at all then you should not expect them to be able to communicate in this manner.
But then how would you explain how the psychics won your gold?
The Bell game requires Alice and Bob to share the entangled Bell state; Rudolph’s improved version requires a slightly more complicated entanglement. Rudolph concludes with a demonstration that even separable quantum states show behaviour that is incompatible with naive realism as defined above. (He also paints Einstein as a naive realist, but on my understanding does not accurately reflect Einstein’s opinions by the end of his life.) Rudolph’s exposition features an entertaining dialogue between Einstein and Pooh Bear. I’ll present it rather more briefly here.
Suppose that Malcolm prepares one of the four states
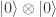 ,
,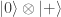 ,
, ,
,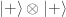 .
.
If, as in naive realism, we do not believe that misty states are themselves real, but instead think that  is really either
is really either  or
or 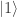 (we just don’t know which until observation), then since any of the four states may give
(we just don’t know which until observation), then since any of the four states may give 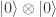 on observation, it is experimentally impossible to learn anything about which state was prepared. This however is false. We calculate that the output of the circuit shown below
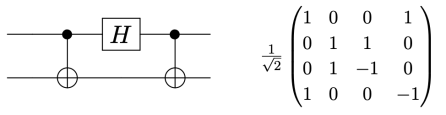
on observation, it is experimentally impossible to learn anything about which state was prepared. This however is false. We calculate that the output of the circuit shown below
is
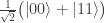 ,
,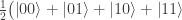 ,
, ,
,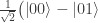 .
.
Now consider what happens when we measure the second qubit in the  -basis.
-basis.
- If it is measured as
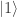 we measure the first qubit in the
we measure the first qubit in the  -basis; if the result of both measurements is
-basis; if the result of both measurements is 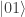 then the initial state was not (1), if is
then the initial state was not (1), if is  then the initial state was not (4).
then the initial state was not (4).
- If instead the second qubit is measured as
 then we apply a Hadamard gate to the first qubit, giving (1)
then we apply a Hadamard gate to the first qubit, giving (1)  , (2)
, (2)  , (3)
, (3) 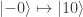 , (4)
, (4)  , and then measure the first qubit in the
, and then measure the first qubit in the  -basis. Now from cases (2) and (3) we see that if the result of both measurements is
-basis. Now from cases (2) and (3) we see that if the result of both measurements is  the initial state was not (3), and if it is
the initial state was not (3), and if it is 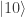 the initial state was not (2).
the initial state was not (2).
Therefore in all cases something can be deduced about the initial state.
Rudolph clearly explains that this result is inconsistent with naive realism but consistent with the view that physical states correspond to unique misty states. But, like Einstein, Rudolph finds the consequences of this, in particularly non-locality, hard to swallow. He concludes (page 139):
I personally live in cognitive dissonance: on a day-to-day basis I talk about the physical properties of the photons … as if they are as tangible as any of the physical properties of the human-scale objects in the room around me. They are not. I suspect I should treat the misty states as states of knowledge, but to be understood within a more general framework of theories of inference than our present theories find comfortable.
The idea that things may not be precisely as they present themselves to our senses has a long pedigree, going back as far as Plato and his shadows on the cave. Hume says it clearly in Section 118 in Enquiry concerning human understanding:
The table, which we see, seems to diminish, as we remove further from it. But the real table, which exists independently of us, suffers no alteration. If was therefore, nothing buts its image, which as present to the mind.
The tension here between things as they are (ontological properties) and things as they seem to us (epistemological properties) has of course been much debated by philosophers after Hume, most notably Kant with his noumena (or Ding an such) and phenomena. What we have seen in this post is that it may be impossible to maintain this separation: the EPR-paradox, Bell’s game, and Rudolph’s final demonstration all point to a theory in which the physical properties making up a real state includes a unique misty state. Moreover, neither the Stern–Gerlach experiment (with its random deflections), nor the EPR-paradox (with its spooky ‘action at a distance’), nor Rudolph’s final demonstration (quantum effects without initial entanglement) require the real state to be anything more than the misty state. But if this is true, it follows that our observed experience of phenomena cannot be disentangled with the ontological question: what is the nature of things as they really are?
vertices has more edges than the complete bipartite graph with bipartition into two parts of size
, then it contains a triangle. He illustrated the method by instead proving the Erdős–Ko–Rado Theorem, that the maximum size of a family of
-subsets of
such that any two members of the family have a non-trivial intersection is
.
we need to prove the Erdős–Ko–Rado Theorem is the Kneser graph, having as its vertices the
-subsets of
. Two subsets
and
are connected by an edge if and only if
. The Erdős–Ko–Rado Theorem is then the claim that the maximum size of an independent set in
is
. As we shall see below, this follows from the Hoffman bound, that an independent set in a
-regular graph on
vertices with adjacent matrix
and least eigenvalue
has size at most
. (Note that since the sum of the eigenvalues is the trace of the adjacency matrix, namely
, and the largest eigenvalue is the degree
, the least eigenvalue is certainly negative.)
, Ehud and his coauthors use the representation theory of the symmetric group. Let
be the permutation module of
acting on the
-subsets of
. It is well known that
has character
into Specht modules,
acts as a linear map on
that commutes with the
-action. Therefore, by Schur’s Lemma, for each
with
there is a scalar
such that
acts on
as multiplication by
. Thus the
are the eigenvalues (possibly with repetition, but this turns out not to be the case) of
.
acts on
by scalar multiplication by
.
has a filtration
and
for
. The submodule
is spanned by certain ‘partially symmetrized’ polytabloids. Rather than introduce this notation, which is a bit awkward for a blog post, let me instead suppose that
acts on the set
where
. Let
be a fixed
-subset of
. Then
is a cyclic
-submodule of
generated (using right modules) by
where
which — viewing
as a submodule of the permutation module of
acting on
-subsets — is defined on the generator
by
-set
appearing in the expansion of
in the canonical basis of
. Applying the adjacency matrix
sends this
-set to all those
-sets that it does not meet. Hence, after applying
and then
we get a scalar multiple of
precisely from those sets
in the support of
is an
-subset of
not meeting
forbidden elements, hence there are
choices for
. Each comes with sign
.
is the least eigenvalue of
. Putting this into Hoffman’s bound and using that the graph
is regular of degree
, since this is the number of
-subsets of
not meeting
, we get that the maximum size of an independent set is at most
; note one may interpret an
-tabloid as an ordered pair
encoding the path of length 3 with edges
and
. There is a proof of Mantel’s Theorem by double counting using these paths: as Ehud remarked (quoting, if I heard him right, Kalai) ‘It’s very hard not to prove Mantel’s Theorem’.
acts on the set of set partitions of
into
sets each of size
. The corresponding permutation character is multiplicity free: it has the attractive decomposition
, where
is the partition obtained from
by doubling the length of each path. Moreover, my collaborator Rowena Paget has given an explicit Specht filtration of the corresponding permutation module, analogous to the filtration used above of
. So everything is in place to prove a version of the Erdős–Ko–Rado Theorem for perfect matchings. Update. I am grateful to Ehud for pointing out that this has already been done (using slightly different methods) by his coauthor Nathan Lindzey.
and the unipotent representations of the finite general linear group
. Perhaps, one day, this will be explained by defining the symmetric group as a group of automorphisms of a vector space over the field with one element. The analogue of the permutation module
of
acting on
-subsets is the permutation module of
acting on
-subspaces of
. This decomposes as a direct sum of irreducible submodules exactly as in
above, replacing the Specht modules with their
-analogues. So once again the decomposition is multiplicity-free. This suggests there might well be a linear analogue of the Erdős–Ko–Rado Theorem in which we aim to maximize the size of a family of subspaces of
such that any two subspaces have at least a
-dimensional intersection.
-intersecting families. The special case
is that the maximum number of
-dimenional subspaces of
such that any two subspaces have at least a
-dimensional interection is
for
, where the
-binomial coefficient is the number of
-dimensional subspaces of
. Thus the maximum is attained by taking all the subspaces containing a fixed line, in precise analogy with the case for sets. (Note also that if
then any two
-dimensional subspaces have a non-zero intersection.)
is to
where
is an infinite field as the Hecke algebra
is to
.) Chapter 13 of his book has, I think, exactly what we need to prove the analogue of the lemma above. Update: I also just noticed that Section 8.6 of Harmonic analysis on finite groups by Ceccherini-Silberstein, Scarabotti and Tolli, titled ‘The
-Johnson scheme’ is entirely devoted to the Gelfand pair
where
is the maximal parabolic subgroup stabilising a chosen
-dimensional subspace.
and let
be the permutation module of
acting on
-dimensional subspaces of
defined over the complex numbers. For
, let
be the map sending a subspace to the formal linear combination of all
-dimensional subspaces that it contains. The
-Specht module
is then the intersection of the kernels of all the
for
. Moreover if we set
and
and
for
.
has vertices all
-dimensional subspaces of
; two subspaces are adjacent if and only if their intersection is
.
is
.
for
and let
. An arbitrary
-dimensional subspace of
intersecting
in
has the form
and
such subspaces. Taking
we get the result.
when
and
when
by computer calculations. Note also that the
-binomial factor
counts, up to a power of
, the number of
-dimensional complements in
to a fixed subspace of dimension
, in good analogy with the symmetric group case. But it seems some careful analysis of reduced row-echelon forms (like the argument for the degree of
above, but too hard for me to to do in an evening) will be needed to nail down the power of
. Examples 11.7 in James' lecture notes seem helpful.
by scalar multiplication by
.
, and it is
. Putting this into Hoffman’s bound and using that the subspaces graph is regular of degree
as seen above we get that the maximum size of an independent set is at most
-analogue of the spectral results on the Kneser graph motivated by Problem A2 in the 2018 Putnam.



 Posted by mwildon
Posted by mwildon